Lukion pitkän matematiikan kurssi MAA2 on työkalukurssi, jonka taitoja tarvitaan jokseenkin kaikilla tämän kurssin jälkeisillä kursseilla. Kannattaa siis opiskella asiat hyvin 🙂
Kurssikartta
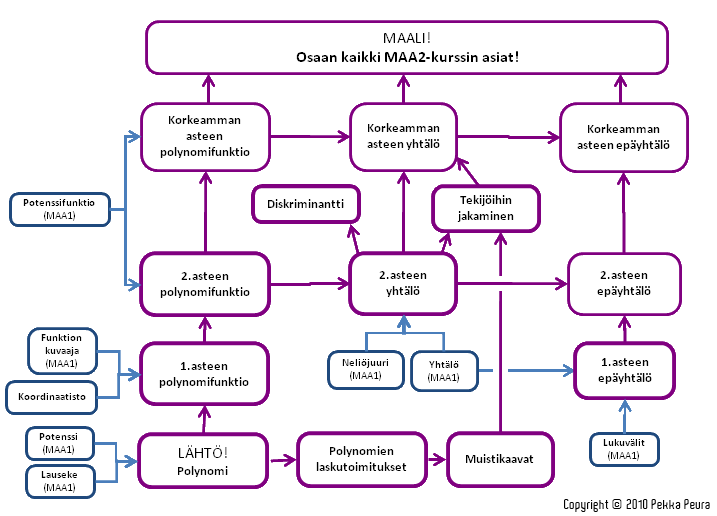
Kurssin tavoitteet
Kurssin tavoitteena on, että opiskelija
- harjaantuu käsittelemään polynomifunktioita
- oppii ratkaisemaan toisen asteen polynomiyhtälöitä ja tutkimaan ratkaisujen lukumäärää
- oppii ratkaisemaan korkeamman asteen polynomiyhtälöitä, jotka voidaan ratkaista ilman polynomien jakolaskua
- oppii ratkaisemaan yksinkertaisia polynomiepäyhtälöitä.
Kurssin keskeiset sisällöt
- polynomien tulo ja binomikaavat
- polynomifunktio
- toisen ja korkeamman asteen polynomiyhtälöitä
- toisen asteen yhtälön juurten lukumäärän tutkiminen
- toisen asteen polynomin jakaminen tekijöihin
- polynomiepäyhtälön ratkaiseminen
Kiitos paljon tästä videosta 🙂 Haluaisn kertoo että nämä video ovat auttaneet minua tosi paljon. Toivon että voisitte laittaa myös puuttuvista kursseista videoita koska pitkämatikka on niin vaikeeta muutenkin niin kiitos kun tuette meitä 🙂
Kiitos palautteesta! Matikan videoita tulee lisää 🙂
Kiitos. Olisi kyllä hyvä saada lisää videoita.
Ole hyvä! uusia videoita tulee jokseenkin päivittäin 🙂
Kurssin kuvauksesta puuttuu sana: oppii ratkaisemaan korkeamman asteen polynomiyhtälöitä, jotka voidaan ratkaista ilman (laskinta..?)
Totta, erittäin hyvä huomio, kiitos! Pitäisi olla ”…ilman polynomien jakolaskua.” 🙂
Nää on ***tanan vaikeita
Kaikki on aluks vaikeeta, mutta kun malttaa tehdä töitä ni kyl ne avautuu
Miten parametri eroaa vakiosta?
Parametri ja vakio voidaan osittain mieltää olevan sama asia vähän tilanteesta riippuen. Tosin esim. matemaattis-luonnontieteellisistä vakioista kuten pii, putouskiihtyvyys g, Avogadron luku jne. ei käytetä termiä ”parametri”. Jossain tilanteissa parametri voidaan ajatella myös muuttujana niin, että funktiossa on useampi kuin yksi muuttuja. Karkeasti ottaen parametri on vähän staattisempi asia kuin muuttuja, mutta ”muuttuvaisempi” kuin esimerkiksi em. luonnontieteelliset vakiot tai lausekkeessa mahdollisesti esiintyvät vakiokertoimet. (Toivottavasti selvensi enemmän kuin sekoitti.)
Otetaan esimerkki: hiihtäjän hiihtonopeus riippuu pääasiallisesti hiihtäjän kunnosta ja hiihtotaidosta. Voidaan ajatella, että hiihtokuntoa ja -taitoa yhteensä kuvaa muuttujan x arvo. Hiihtonopeuteen kuitenkin vaikuttaa myös esimerkiksi lämpötila ja siitä aiheutuva lumen koostumus, käytetty suksivoide ja hiihtäjän elimistössä olevan energian määrä. Siis hiihtonopeuteen ensisijaisesti vaikuttava tekijä on muuttuja x, mutta lämpötila, lumen koostumus, suksivoide ja energiamäärä (joita voitaisiin tässä tilanteessa kutsua sekä parametreiksi että muuttujiksi) täytyy myös huomioida.
onko olemassa lähteitä, joista voi ilmaiseksi lataa lukion e-oppikirjoja?
Tuskin ne on ilmaisia.
Ja niin, kiitos videoista. Nää auttaa kokeisiin todella paljon!
Kiitos palautteesta
Kiitos videoista!
kiitos tästä. Matematiikan opiskelu on taiteilijalle yhtä helvettiä, kun laudat ovat tarhassa sikinsokin ja insinöörin aivoissa ne ovat kaikki loogisesti järjestellyissä nipuissa.
Onko teillä video nollakohtien ja tekijöiden yhteys- aiheesta?