Johdanto tason koordinaatistoihin
Johdanto analyyttiseen tason koordinaatistoihin. Käsitellään esimerkkien kautta tavallista xy-koordinaatistoa (eli karteesista koordinaatistoa; esimerkit 1-2) ja napakoordinaatistoa (esimerkki 3)
- 0:31 Esimerkki 1: xy-koordinaatisto laivanupotuspelissä
- 3:20 Esimerkki 2: xy-koordinaatisto A4-paperilla
- 5:37 Esimerkki 3: suunnistettaessa napakoordinaatistoa tulee käytettyä intuitiivisesti
Muistiinpanot johdannosta

xy-koordinaatisto (eli karteesinen koordinaatisto) tasossa
Videolla käsitellään tavallista xy-koordinaatistoa eli ns. karteesista koordinaatistoa tasossa. Nimitys ”karteesinen” tulee ranskalaisen matemaatikon ja filosofin René Descartes’n nimestä.
Kun pisteen P koordinaatit esitetään, esim. $P = (1,2)$ niin ensimmäinen koordinaatti (tässä arvo 1) tarkoittaa x-akselin kohtaa, jonka ylä- tai alapuolella piste P on ja jälkimmäinen koordinaatti (tässä 2) tarkoittaa minkä y-akselin kohdan vasemmalla tai oikealla puolella piste on. Yhdessä nämä kaksi arvoa lukitsevat pisteen sijainnin.
Huomaa, että jos koordinaattiarvoista jompi kumpi tai molemmat ovat desimaalilukuja, käytetään koordinaattiarvoja toisistaan erottavana merkkinä sekaannuksen välttämiseksi pilkun sijasta puolipistettä. Esim. $Q = (1,37; -2,53)$.
Huomaa edelleen, että englantilaiset ja amerikkalaiset käyttävät desimaalipistettä, ei -pilkkua. Tällöin em. pisteen Q esitys olisi $Q = (1.37, -2.53)$. Tämä on tärkeää tietää, sillä tietokoneohjelmia käytettäessä on usein tästä syystä käytettävä nimenomaan *desimaalipistettä*.
Muistiinpanot xy-koordinaatistosta


Napakoordinaatisto tasossa
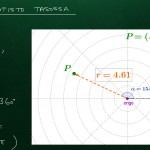
Tutun xy-koordinaatiston (eli karteesisen koordinaatiston) ohella napakoordinaatisto on hyödyllinen tapa esittää tason pisteitä. Käytämme itseasiassa napakoordinaatistoa täysin intuitiivisesti antaessamme ihmiselle reittiohjeita: ”kulje suoraan siihen ja siihen suuntaan niin ja niin kauan.” Edellinen ilmaus käytännössä kertoo määränpään koordinaatit napakoordinaatistossa, jonka origona on lähtöpiste ja nollasuuntana esimerkiksi karttapohjoinen (nollasuunnan kiinnitys riippuu tosin paljolti käyttötilanteesta).
Napakoordinaatistossa siis ilmaistaan piste seuraavasti: $P = (r, \alpha)$, missä $r$ on etäisyys origosta ja $\alpha$ on valitusta nollasuunnasta (laskuissa yleensä xy-koordinaatiston x-akselin positiviinen puoli) mitattu kulma.
Muistiinpanot napakoordinaatistosta
Mikäs se matemaatikon vitsi ois 😀
Kerro se vitsi! Ei saa jättää roikkumaan 😀
Eiku veikkaan itse. Oisko ”Matemaatikko eks yy koordinaatistoon”?