Huomaa, että toisin kuin yhtälöitä käsiteltäessä, epäyhtälöiden (ja siis myös itseisarvoepäyhtälöiden) ratkaisut ovat usein äärettömän monesta pisteestä koostuvia joukkoja. Esimerkiksi jos epäyhtälön ratkaisuksi saataisiin $x\geq 5$, tarkoittaa tämä, että luku 5 ja kaikki sitä suuremmat reaalilukuarvot olisivat tällöin osa ratkaisujoukkoa.
Itseisarvoepäyhtälön ratkaiseminen graafisesti
Tämä lähestymistapa on erittäin hyvä tuloksen hahmottelemiseen ja tarkistamiseen.
Muistiinpanot

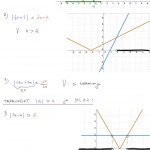
Itseisarvoepäyhtälöesimerkki 1
Ratkaistaan ”lokeroimalla” epäyhtälö $|2x+4|\leq 6$.
Muistiinpanot


Itseisarvoepäyhtälöesimerkki 2
Ratkaistaan edellistä tilannetta hiukan haastavampi epäyhtälö $|-x-3| > |x^2-2x-3|-4$ myöskin ”lokeroimalla”.
Muistiinpanot


Mistä tuon abs merkin löytää piirtovalikossa? Yritin ettiä käyttöohjeista mutta ei löytyny!
Riippuu laskimesta, mutta esim Casion graafisissa laskimissa OPTN-napin alta.
Suuri kiitos lokerointimenetelmän opettamisesta, selkeytti itseisarvoyhtälöiden ja -epäyhtälöiden ratkaisemista kummasti!
Cool! Itseisarvoyhtälöt on vähän hazardeja ymmärtää ilman ”lokerointia” kyllä 🙂 Omalta osaltani kiitos ko. menetelmän oppimisesta menee entiselle kollegalleni Sakari Svärdille Kuopioon.