Johdanto
Johdattelua potenssifunktion ja juurifunktion väliseen yhteyteen siinä tilanteessa kun potenssifunktiossa eksponenttina on positiivinen kokonaisluku.
Muistiinpanot
Pariton juurifunktio
Teoriaa
Johdetaan pariton juurifunktio parittoman potenssifunktion kautta.
Muistiinpanot


Esimerkkejä parittomista juuriyhtälöistä ja -epäyhtäöistä
0:06 Funktion $f(x) = \sqrt[3]{x+5}$ määrittelyjoukko
0:50 Kuten edellä, mutta $f(x) = \frac{1}{\sqrt[5]{2x-3}}$
1:50 Kuten edellä, mutta $f(x) = \frac{3x}{\sqrt[7]{x^2+1}}$
2:40 Ratkaise yhtälö: $\sqrt[5]{3x+1} = -2$
3:24 Ratkaise epäyhtälö: $\sqrt[3]{4x^2+5x} < 2x$
Muistiinpanot


Parillinen juurifunktio
Teoriaa
Tutkitaan parillista juurifunktiota parillisen potenssifunktion käänteisfunktiona. Huomaa, että parillisen potenssifunktion lähtö- ja maalijoukkoja on rajoitettava, jotta käänteisfunktio (eli parillinen juurifunktio) olisi olemassa.
Muistiinpanot
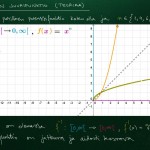
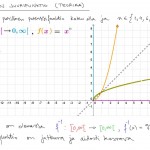
Eikö kohdan 2.2 viimeisen esimerkin vastauksessa olevien -2 + 2 sqrt(11) ja -2 – 2 sqrt(11) tilalla pitäisi olla 1/4 + 1/4 sqrt(11) ja 1/4 – 1/4 sqrt(11)?
Joo, kyllä, kiitos huomiosta! Pitäisi olla just noin kuten sanoit 🙂 Näköjään multa on jäänyt ratkaisukaavan nimittäjästä kerroin (-8) pois, tai ainakin sillä virheellä saa tuollaiset tulokset aikaan. Laitan muistiin, että video täytyisi korjata, mutta tässä vaiheessa lisään YouTube-kommentin aiheesta videoon.
Minkä takia videossa 2.2 esimerkki c):ssä ovat kaikki luvut mahdollisia ja b):ssä tämä määritellään? Eli siis miksi c):ssä ei tehdä: x^2+1 saa olla +-1? Onko nimenomaan sen takia, että se ei yksinkertaisesti voi olla parillisen potenssin takia+-1?
Tarkoitin siis x^2+1 EI saa olla +-1