Teoriaa, kuvaajan tarkastelua ja ominaisuuksia
Logaritmifunktio on eksponenttifunktion käänteisfunktio. Videolla tarkastellaan logaritmifunktion kuvaajan yhteyttä käänteisfunktionsa (eli vastaavan eksponettifunktion) kuvaajaan. Lisäksi mietitään logaritmifunktion määrittely- ja arvojoukkoa sekä aitoa monotonisuutta (eli aidosti kasvavuutta/aidosti vähenevyyttä).
Muistiinpanot
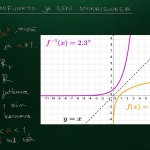
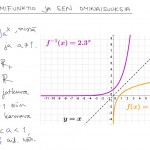
Logaritmifunktio ja eksponenttifunktio määrittely- ja maalijoukkoineen
- a-kantainen logaritmifunktio: $f:\;]0,\infty[\;\to\mathbb{R}, f(x)=\log_a x$
- a-kantainen eksponenttifunktio: $g:\mathbb{R}\to\;]0,\infty[\;, g(x)=a^x$
YO-esimerkkejä logaritmien määrittelyehdoista
Videolla tutkitaan kahta vanhaa ylioppilastehtävä (K2007:9 ja K1997:3b) liittyen logaritmifunktioiden määrittelyehtoihin.
Muistiinpanot


Lisää esimerkkejä
Videolla tehdään kolme esimerkkiä:
0:07 Logaritmeihin liittyvä todistustehtävä
3:10 Aitoa monotonisuutta hyödyntävä ”Kumpi on suurempi?” -vertailu
5:30 Logaritmeja sisältävä raja-arvolasku
Muistiinpanot


Sivun ensimmäisessä videossa ”Logaritmifunktion teoriaa ja ominaisuuksia” on virhe noin ajassa 3:30. Pitäisi olla f^(-1)(4) eikä f^(-1)(2). Pystyisikö korjaamaan, etteivät opiskelijat mene sekaisin? Kiitos mahtavista videoista!
Moikka Paula! Pahoittelut virheestä, lisäsin videoon kommentin aiheesta 🙂 Valitettavasti kommentti ei näy mobiililaitteella videota katsottaessa. Ja kiitos palautteesta 🙂