Polynomi jakokulmassa (esim 1)
Polynomin jakaminen polynomilla jakokulmassa, esimerkki 1: $\frac{x^3+2x^2-5x-6}{x+1} = x^2 + x – 6$.


Polynomi jakokulmassa (esim 2)
Polynomin jakaminen polynomilla jakokulmassa, esimerkki 2: $\frac{2x^3-14x-12}{x-2} = 2x^2 + 4x – 6$.
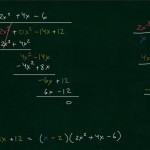
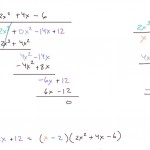
Polynomi jakokulmassa (esim 3)
Polynomin jakaminen polynomilla jakokulmassa, esimerkki 3: $\frac{0.5x^3+x}{2x+1} = \frac{1}{4}x^2 + \frac{1}{8}x + \frac{9}{16}$, jakojäännös $-\frac{9}{16}$.

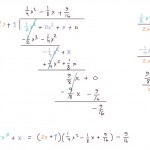
Mikä tuon liitutaulu ohjelman nimi on? Mitä ohjelmaa käytät videoissasi?
Morjes Erkka! Noi on ihan kuvankäsittelyohjelmalla, esim. SmoothDraw on ilmainen
Hei! Onko jotain hyvää ideaa mitä tehdä, kun jakaja (tai jaettava) on neliöjuuressa?
PS. Kiitos loistavasta sivusta!
Riippuu lausekkeesta; antaisitko esimerkin?
2014-04-20 18:48 GMT+03:00 Disqus :
Jaettavana 2x^2+2 jakajana neliöjuuren sisällä x^2+1
Hallelujah, taas nää videot pelastaa! Kiitos kaunis!
Hei! Pohdiskelin tässä että esimerkissä 2 kuuluisiko vakiotermin olla -12. Sillä videolla se on + 12. Kun loppuvaiheilla kerrot -2*-6 tulos olisi +12 ja jäisi tämän jälkeen +24 jakojäännökseksi. Onko siis merkkivirhe vai olenko itse pudonnut kärryiltä:D? PS. Jos joku on pelastanut minun matikanopiskelun niin nämä videot! Kiitos.
Janne hoitaa vähennyslaskun siten että kirjoittaa aina kertolaskun tuloksen vastakkaismerkkisenä ja sitten laskee termejä yhteen. Eli siis (-2)*(-6) = 12, mutta se kirjoitetaan -12. Vertaa saman rivin edelliseen termiin: Siinä oli kertolaskun tulos -6 * x = -6x, ja se vastakkaismerkkisenä 6x.
Voitko selittää mistä päättelet jakajan merkit, eli onko se x-1 vai x+1?