Käänteisfunktio

Johdanto: Caesar-salaus ja käänteisfunktio

Johdatellaan käänteisfunktioiden perusidea historiallisesti merkittävän Caesarin salauksen eli Caesarin siirron avulla. Salakirjoituksen murtaminen on tavallaan käänteisfunktion etsimistä alkuperäiselle salauksen muodostaneelle funktiolle (ja menetelmästä riippuen syötetyille lisäparametreille).

Mikäli salakirjoitusaihe kiinnostaa enemmänkin, erittäin suositeltavia kirjoja ovat esim. Simon Singhin Koodikirja ja F. W. Winterbothamin Operaatio Ultra.

Käänteisfunktion määritelmä ja olemassaolo

Funktiolla $f:A\to B$ on olemassa käänteisfunktio $f^{-1}:B\to A$ mikäli kaikilla $x\in A$ pätee $f^{-1}(f(x)) = x$. Tällöin väistämättä pätee myös kaikilla $y\in B$, että $f(f^{-1}(y)) = y$.

Muistiinpanot

Milloin funktiolla on käänteisfunktio?

Tutkitaan funktiota $f(x)=x^2$ ja muutellaan sen määrittely- ja maalijoukkoa. Milloin funktiolla on olemassa käänteisfunktio? Tämä video havainnollistaa sitä miksi funktioita tarkasteltaessa määrittely- ja maalijoukon valinta ei ole yhdentekevää.

Muistiinpanot

Huomautuksia

xy-koordinaatistoon piirretyllä funktiolla $y=f(x)$ ei ole käänteisfunktiota mikäli kuvaajaan voi piirtää…

• vaakasuoran viivan, joka leikkaa kuvaajaa useammin kuin kerran (sillä f ei tällöin ole injektio).
• jollekin maalijoukkoon kuuluvalle korkeudelle vaakasuoran, joka ei leikkaa kuvaajaa ollenkaan (sillä f ei tällöin ole surjektio).

Aidosti kasvavalla funktiolla on aina aidosti kasvava käänteisfunktio. (Aidosti vähenevälle funktiolle vastaavasti.) Jos lisäksi funktio on jatkuva ja määritelty välillä (esim. nollasta neljään) niin käänteisfunktio on jatkuva.

Funktio sen ja käänteisfunktio samassa kuvassa

Jos funktiolla on olemassa käänteisfunktio niin samaan kuvaan piirrettynä kuvaajat ovat toistensa peilikuvia suoran y=x suhteen.

Muistiinpanot

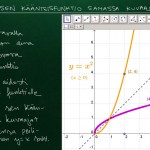
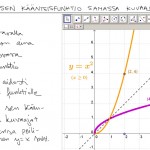
Esimerkki käänteifunktion määrityksestä

Osoitetaan, että funktiolla $f:[1,4]\to \mathbb{R}, f(x)=\tfrac{1}{2}x^3$ on (maalijoukkoa rajaamalla) olemassa käänteisfunktio ja määritetään sen lauseke.

Muistiinpanot