Teoria-taustaa
Käsitellään teoriataustaa eksponenttiyhtälöiden ratkaisemiseen liittyen. Yleensä eksponenttiyhtälöitä ja -epäyhtälöitä ratkaistaan logaritmeja hyödyntämällä, mutta koska logaritmia ei vielä ole käsitelty, käydään ensin asiaa läpi ilman logaritmien apua ymmärryksen syventämiseksi.
Muistiinpanot


Esimerkkejä eksponenttiyhtälöistä ilman logaritmia
Käsitellään ensin ohjeet siitä kuinka eksponenttiyhtälöitä ratkaistaan ilman logaritmeja. Tämän jälkeen tehdään neljä esimerkkiä aiheesta:
0:15 Ohjeet muotoa $a^x=b$ olevien yhtälöiden ratkaisemiseen ilman logaritmeja
3:13 Esimerkki a: $2^{3x} = 64$
5:35 Esimerkki b: $\left(\frac{2}{3}\right)^x = \frac{27}{8}$
8:48 Esimerkki c: $5^{3-x} = 125 \cdot 25^{\tfrac{1}{2}x+2}$
11:50 Esimerkki d: $2^{2x+1} – 9\cdot 2^x – 4 = 0$
Muistiinpanot


Esimerkkejä eksponenttiepäyhtälöistä ilman logaritmia
Eksponenttiepäyhtälöiden ratkaiseminen ilman logaritmeja menee samoilla periaatteilla kuin vastaavien yhtälöidenkin ratkaiseminen. Ainoa tärkeä ero epäyhtälömerkin suunnan kääntyminen kantaluvun arvosta riippuen (ks. videolta tarkemmin).
Muistiinpanot
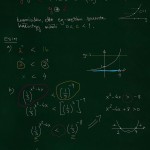

Mitäs sitten jos c (kun funktio on muotoa c^x) onkin negatiivinen?
Yleisen sopimuksen mukaan eksponenttifunktio on määritelty vain positiivisilla kantaluvuilla johtuen siitä, että negatiivisten kantalukujen tapauksessa päädytään nopeasti huonosti määriteltävissä oleviin tilanteisiin.
Esimerkkinä edellisestä: jos c=-16 niin tällöin jos olisi x=1/2=2/4 niin (-16)^(1/2) ei ole määritelty (reaalilukujen joukossa), mutta (-16)^(2/4) = 4 mikäli käytetään laskujärjestystä ((-16)^2)^(1/4). Eri laskujärjestystä käytettäessä jälkimmäinen ei myöskään ole määritelty (reaalilukujen joukossa). Kuitenkin koska 1/2=2/4 niin olisi toivottavaa, että lopputulos olisi aina sama.
Kuitenkin jos hyväksytään, että kantaluku c on kompleksiluku, ei ongelmia synny ja tulos em. laskuista on yksikäsitteinen 0+4i=4i.
MIten on mahdollistä että 3-x muuttuu jotenkin yht äkkiä -2x. toisen videon c tehtävässä?
Siinä siirrellään termejä yhtälön molemmin puolin. Eli 3 siirtyy oikealle (vähennetään siitä 7:stä jolloin saadaan 4) ja oikealta siirtyy toinen x vasemmalle, eli tulee -x-x = -2x. Eli normaalia yhtälön ratkaisemista 🙂
Mistä tuo 2. asteen yhtälön Y saa arvokseen -9? (2. videolla, viimeinen lasku)