Teoriaa diskriminantista toisen asteen polynomille
Toisen asteen yhtälön ($ax^2+bx+c=0$) ratkaisukaavassa neliöjuuren sisällä olevaa osaa kutsutaan diskriminantiksi. Diskriminantin arvosta nähdään suoraan montako ratkaisua 2. asteen yhtälöllä on:
- Jos D < 0, niin alkuperäisellä 2. asteen yhtälöllä ei ole ratkaisuja
- Jos D = 0, niin ratkaisuja on tasan yksi
- Jos D > 0, niin ratkaisuja on tasan kaksi
Muistiinpanot
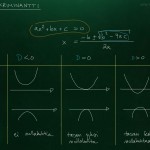
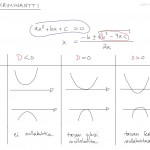
Esimerkkejä diskriminantin hyödyntämisestä
- 0:30 Montako ratkaisua yhtälöllä $2x^2 + 3x – 4 = 0$ on?
- 2:37 Osoita, että funktio $f(x) = -x^2 + 2x – 4$ saa vain negatiivisia arvoja
- 4:36 Millä vakion k arvolla yhtälöllä $6x^2+4kx+2k=0$ on kaksoisjuuri?
Muistiinpanot


Miten lasketaan: Millä vakion a arvoilla funktio f(x) = -x(potenssiin kaksi) +ax+a-3 saa vain negatiivisia arvoja?
Moikka, tarkotat ilmeisesti: f(x) = -x^2 + ax + a – 3 vai f(x) = (-x)^2 + ax + a – 3 ? Koska toisen asteen termin kerroin on negatiivinen (-1) niin täytyy olla niin, ettei funktiolla f ole yhtään nollakohtaa ja kuvaaja olisi näin ollen alaspäin aukeava paraabeli, joka on kokonaan x-akselin alapuolella. Toisen asteen polynomifunktiolla ei ole nollakohtia täsmälleen silloin, kun diskriminantti on negatiivinen.
Älä sotke diskriminantin kaavassa olevia a, b ja c tämän funktion f kertoimiin! Diskriminantin kaavassa a tarkoittaa siis 2. asteen termin kerrointa, b on 1. asteen termin kerroin ja c on vakiotermi. Siis tässä esitetyn funktion f kertoimilla diskriminantin on oltava: a^2 – 4*(-1)*(a-3) < 0. Huomaa, että vakiotermi on koko lauseke (a-3). Eli pääset tuossa lopulta ratkaisemaan 2. asteen epäyhtälön a:n suhteen.
Moi! Miten lasketaan: Millä parametrin k arvoilla yhtälön (k-1)x toiseen-5x=-1 reaalijuurten lukumäärä on
a) yksi b) nolla c) kaksi?
Moikka Saara! Kirjoita yhtälö muotoon (k-1)x^2 – 5x + 1 = 0 ja mieti sen jälkeen mikä on diskriminantin lauseke ja ratkaise tämän jälkeen millä k:n arvoilla diskriminantti on a) nolla, b) negatiivinen, c) positiivinen.
Moro! Tehtävä Pitkä matematiikka 2 kirjasta: Määritä vakiolle q sellainen arvo, että funktioiden f(x)=x^2+3x+q ja g(x)=-x^2+x kuvajilla on vain yksi yhteinen piste.
Sain oikean vastauksen kyllä, mutta ilman ymmärrystä. Eli merkitsin funktioiden arvot yhtäsuuriksi ja päädyin yhtälöön 2x^2-2x+q=0. Tästä sitten ihan normaalisti diskriminantti nollaksi kirjoittamalla sain vastaukseksi q=0,5.
Pyrin aina miettimään, mitä tehtävä tarkoittaa kuvaajan kannalta, jotta hahmottaisin sen paremmin ja tässä kohtaa ajatus tökkää. Ensin käsitellään kahta kuvaajaa, joista päädytään yhtälöä ratkaistaessa yhdeksi kuvaajaksi, joka sitten kertoo, että funktio f(x)=2x^2-2x+q saa vain epänegatiivisia arvoja, kun q:n arvo on 0,5. Eli lyhyesti: Miksi ratkaisemalla tehtävä kuten sen ratkaisin, saadaan selville sellainen q:n arvo, jotta kuvaajilla olisi vain yksi yhteinen piste.
En pääse kysymään tästä kotiopiskelijana keltään niin olisin hyvin kiitollinen vastauksesta!
Moikka! Ensimmäisenä tulee mieleen, että ota GeoGebra-niminen ohjelma käyttöön, luo ikkunaan liukusäädin ja anna sen nimeksi q. Tämän jälkeen syötä ikkunan alareunassa olevaan syötekenttään juuri näin: f(x)=x^2+3x+q (ja paina Enter) sekä g(x)=-x^2+x. Tämän jälkeen vaihtele q:n arvoja liukusäätimellä; huomaat mitä tapahtuu. Yhtälön f(x)=g(x) tarkastelua varten voit halutessasi luoda lisäksi myös funktion h(x)=f(x)-g(x) (tai vaihtoehtoisesti h(x)=g(x)-f(x)) niin huomaat ehkä yhteyden kun muuttelet q:n arvoa liukusäätimestä vielä lisää.
Oliko selityksestä apua?
Heippa! Tämmöinen kysymys olisi, että miten lasketaan:
Keksi esimerkki toisen asteen yhtälöstä, jos diskriminantti on a.) 5 ja b.) -2.
Keksi a, b ja c niin, että lausekkeen b^2 – 4ac arvo on a) 5 ja b) -2. (Lisäksi, jotta kyseessä olisi 2. asteen polynomi niin kertoimen a täytyy olla nollasta poikkeava.)
Todella selkeitä videoita, kiitos paljon!
7.15; kyllä saa kuudentoista yhteiseksi tekijäksi, 4 ei vain ole oikea kerroin 😉