Jatkuviin funktioihin liittyviä lauseita (mm. Bolzano)

Bolzanon lauseen teoriaa

Käsitellään Bolzanon lausetta, jonka mukaan

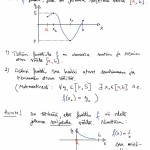
1. jos funktio on jatkuva suljetulla välillä $[a,b]$  ja
2. funktio saa välin $[a,b]$  päätepisteissä erimerkkiset arvot (eli $f(a) \cdot f(b) < 0$)

niin tällöin funktiolla on ainakin yksi nollakohta avoimella välillä $]a,b[$.

Muistiinpanot

Huom!

• Bolzanon lausetta hyödynnetään mm. funktion nollakohtien (eli yhtälön ratkaisujen) olemassaolon tutkimisessa tilanteissa: on olemassa yhtälöitä, joita ei voi ratkaista analyyttisesti (eli kynä-paperi -menetelmällä) vaan on tyydyttävä numeeriseen likiarvoratkaisuun (vrt. numeeristen menetelmien kurssi). Tällöin on erittäin hyödyllistä tietää, että ratkaisu on ylipäänsä olemassa tietyllä välillä, jolloin numeerista ratkaisumenetelmää voidaan soveltaa ko. välille rajoittuen.
• Funktion on ehdottomasti oltava jatkuva suljetulla välillä, jotta Bolzanon lausetta voi hyödyntää. Esimerkkinä vaikkapa funktio $f(x)=\frac{1}{x}$. Kyseinen funktio on jatkuva koko määrittelyjoukossaan (eli kun $x\neq 0$) ja saa erimerkkiset arvot esim. suljetun välin $[-1,1]$ päätepisteissä. Silti funktiolla ei ole yhtään nollakohtaa välillä $]-1,1[$ (eikä tarkemmin sanoen missään muuallakaan). Näin siksi, että kohdassa $x=0$, eli kun funktio ei ole määritelty, se ”hyppää” x-akselin yli (piirrä kuvaaja esim. laskimella tai GeoGebralla).
• Bolzanon lause on itseasiassa erikoistapaus jatkuvien funktioiden väliarvolauseesta.

Esimerkki Bolzanon lauseen hyödyntämisestä

Tehdään esimerkki Bolzanon lauseen hyödyntämisestä funktion nollakohtien lukumäärän tutkimisessa.

Jatkuvien funktioiden väliarvolause

Jatkuvien funktioiden väliarvolauseen mukaan funktiolla, joka on jatkuva suljetulla välillä, on olemassa suurin ja pienin arvo kyseisellä välillä. Lisäksi funktio kaikki ko. välillä olevan suurimman ja pienimmän korkeusarvon välissä olevat arvot.

Muistiinpanot

Huom!

1. Bolzanon lause on itse asiassa tämän asian erikoistapaus.
2. On oleellista, että funktio on jatkuva suljetulla välillä. Jos väli on edes toisesta päästä avoin, voi tulla ongelmia, kuten videon lopussa oleva esimerkki funktiolla $f(x) = \frac{1}{x}$ osoittaa.

Esimerkkejä jatkuvien funktioiden väliarvolauseesta

Tehdään kolme esimerkkiä aiheesta.

• Ensimmäisessä tutkitaan aidosti kasvavan funktion arvojoukkoa
• Toisessa ja kolmannessa vastaesimerkkejä tilanteista, joissa jatkuvien funktioiden väliarvolause ei päde (eri syistä)

(HUOM! Videon lopussa esimerkissä 3 on virhe kun väitetään, että ”R ei ole suljettu”. Se on kyllä suljettu, mutta ei rajoitettu. Tähän tulee korjaus.)