Johdanto toispuoleisiin raja-arvoihin
Sovelletaan (jokseenkin keinotekoisesti) suunnistusesimerkkiä toispuoleisten raja-arvojen käsitteen johdatteluun 🙂
Toispuoleiset raja-arvot GeoGebran avulla
Toispuoleisten raja-arvojen käsitteen esittely GeoGebra-ohjelman avulla. Lisäksi esitellään aiheeseen liittyvät matemaattiset merkinnät.
Toispuoleisia raja-arvoja tarvitaan raja-arvon ja sitä kautta jatkuvuuden ja derivaatan määrittelyssä.
Muistiinpanot toispuoleisista raja-arvoista
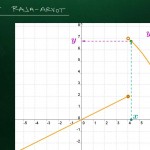
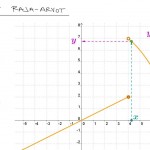
Raja-arvon määritelmä esimerkin avulla
Funktiolla $f$ on olemassa raja-arvo kohdassa $x_0$, mikäli sillä on olemassa toispuoleiset raja-arvot $x_0$:ssa JA toispuoleiset raja-arvot ovat yhtä suuret.
Muistiinpanot raja-arvon määritelmästä
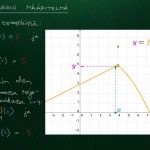
Raja-arvo teoreettisemmin ja esimerkkejä
Raja-arvon määritelmä vielä kertaalleen hiukan symbolisemmin orientoituneesti. Lisäksi neljä esimerkkiä raja-arvon määrittämisestä kuvaajan perusteella.
Muistiinpanot
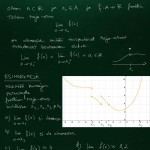
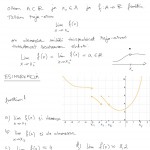
Huomautus
Ei tämän kurssin asia, mutta: tarkasteltaessa funktion raja-arvoa kun x lähestyy ääretöntä (tai miinus ääretöntä), älä puhu oikeanpuoleisesta (vasemmanpuoleisesta) raja-arvosta. Mieti mikä absurdius kyseisiin ilmaisuihin sisältyisi, jos niitä käyttäisi.
Tuosta suunnistusesimerkistä jäi hieman hampaankoloon. En ollut mikään maailman paras suunnistaja koulussa tai intissä. Muutama rasti välillä jäi löytämättä eikä juoksunopeus ollut paras mahdollinen mutta kyllähän sitä on kompassin ja kartan kanssa jotenkuten pärjätty kun on ollut pakko.
Se että, et juokse korkeuskäyröjä vastaan, ei vielä tee maastosta tasamaata. Maasto on sitä, mitä kartassa lukee. (toivottavasti, sillä tarkka kartta on mitä hyödyllisin apuväline suunnistuksessa!).
Et juokse ylämäkeen, etkä juokse alamäkeen, vaan juokset sivuttain mäessä, silloin kun juokset korkeuskäyrän suuntaisesti. Tämä edellinen ei tarkoita kansanomaisessa kielenkäytössä tasamaata,
tasamaa tarkoittaa laakeata maastoa esim tundra, tai aavikko tai aukea.
Sivuttain mäessä tarkoittaa, että toinen puoli on korkeammalla kuin toinen puoli (kuvittele
että juokset mäessä sivuttain, niin että vasen jalka on korkeammalla
kuin oikea jalka, toisinsanoen vasen jalka on ylämäen puolella). Eihän sitä voi kansanomaisesti oikein sanoa ”tasamaaksi” koska täytyy varoa ettei kompastu mäessä ja tipu alas!
Kokeile itse juosta sivuttain jyrkässä mäessä. Ei se ole aina niin helppoa! 😀
Korkeuskäyrät vain kuvaavat käsittääksen mäen korkeuden muutosta, sekä itse mäen korkeutta muuhun kartan maastoon nähden. Kyse on viime kädessä arviosta ja mallinnuksesta mäen korkeuden suhteen, koska korkeusulottuvuus puuttuu kaksiulotteisesta paperikartasta. Tiheästi esiintyvät (useammat) korkeuskäyrät tarkoittavat jyrkempää mäkeä, kun taas harva määrä korkeuskäyröjä tarkoittaa lievää mäkeä.
Morjes ja kiitos kommentista 🙂
Kyllä, oot oikeassa, korkeuskäyrien suuntaan juokseminen ei tarkoita tasamaata sanan perinteisessä merkityksessä merkityksessä: määrittelisit varmaankin näin: piste x on tasamaalla kolmiulotteisessa tilassa mikäli on olemassa säde r > 0 siten, että pisteestä x mihin tahansa suuntaan säteen r etäisyydellä olevaan maanpinnan pisteeseen piirretty sekantti on kohtisuorassa maan vetovoimavektoria vastaan.
Kun videolla sanoin, että juostaan tasamaalla, ajattelin asiaa nimenomaan etenemissuuntaan nähden, jolloin korkeus ei (juurikaan) muutu eli (suuntais)derivaatan arvo kyseiseen suuntaan edettäessä on nolla; siis kyseessä on tasamaa *liikesuunnan* suhteen.
Eli puhutaan samasta asiasta vähän eri termeillä 🙂
Noni Juha88 . Toivottavasti olet nyt näin vuoden jälkeen saanut tuon sitruunan perseestäsi mikä ihan selvästi sielä ainakin on ollut.