Jatkuvan funktion raja-arvon määrittäminen
Raja-arvon määrittäminen jatkuvalle funktiolle yksinkertaisesti sijoittamalla raja-pisteen arvo funktion lausekkeeseen. Perustelut tälle käsitellään myöhemmin jatkuvan funktion määritelmästä puhuttaessa.
Jatkuvuutta ei varsinaisesti ole vielä käsitelty. Mielikuvana funktion jatkuvuus kuitenkin on sitä, että kuvaajan voi piirtää niin, että kynän saa nostaa paperista irti korkeintaan sellaisissa kohdissa, joissa funktio ei ole määritelty.
Muistiinpanot
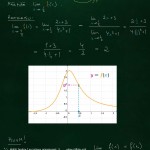

Esimerkkejä raja-arvolaskuista, osa 1
Tehdään kaksi esimerkkiä raja-arvolaskuista, joissa lähtötilanne on muotoa $\dfrac{0}{0}$: tällöin osoittajasta ja nimittäjästä löydetään esim. muistiikaavojen tai muulla tavalla tekijöihin jakamalla yhteisiä tekijöitä, jotka voi supistaa pois.
Muistiinpanot
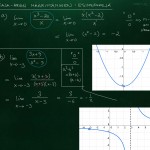

Esimerkkejä raja-arvolaskuista, osa 2
Hiukan edellistä monimutkaisempi raja-arvolasku:
Muistiinpanot


Raja-arvon laskusäännöt
Käsitellään raja-arvojen laskusäännöt, joita edellisissä videoissa surutta hyödynnettiin. Näin tarkasti ei laskuissa tarvitse asioita yleensä esittää ellei erikseen pyydetä. Taustoja on hyvä kuitenkin tietää.
Muistiinpanot


Pyramidi kirja sarjan esimerkeissä oli käytetty tota tekijöihin jakoa nollakohtien avulla myös tässä derivaatta kurssissa, mutta olin jo unohtanut sen. Olin aivan pihalla, kun kirja käytti esimerkeissään kyseistä tapaa jakaa polynomi tekijöihin, mutta ei näyttänyt miten se tapahtuu. Nyt vasta katsottuani nämä videot tuli mieleen toi tekijöihin jako nollakohtien avulla ja koin ”ahaa” elämyksen ! Nämä videot on todella iso apu tuskaisiin koe viikkoihin !!
Toivottavasti meni koeviikko hyvin 🙂
-kiitos munkin puolesta, asiat on selkeästi esitetty. Mahtaa olla rankkaa puhua & opettaa koneelle, vai onko nämä tehty samanaikaisesti oikean luokan edessä?^_^
Kiitos palautteesta! Ei oo tehty luokkatilanteessa vaan erikseen nauhoittaen 🙂