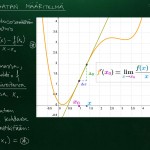
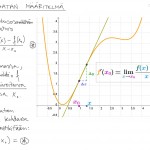
Derivaatta määritellään raja-arvoa hyödyntäen: muodostetaan käyrälle sekantti (suora kahden käyrän pisteen kautta) ja sitten ”liikutetaan” yksi pisteistä ”tosi lähelle” toista. Raja-arvona saadaan tangentti, jonka kulmakertoimesta olemme nyt kiinnostuneita.
Derivaatta kohdassa $x_0$
Käsitellään ensin derivaattaa kuvaajan tasolla GeoGebran avulla ja määritellään sen jälkeen derivaattalauseke erotusosamäärän raja-arvon avulla kohdassa $x_0$.
Muistiinpanot
Derivaatan määritelmä h-parametrin avulla
Usein derivaatan määritelmä esitetään seuraavassa muodossa:
Esimerkkejä edellisen määritelmän hyödyntämisestä
Lasketaan derivaatan ”h-määritelmän” avulla funktioiden $f(x)=x^2$ ja $g(x)=\dfrac{1}{x^2+2}$ derivaatat $f'(-1)$ ja $g'(1)$.
Muistiinpanot


Erinomaiset videot derivaatasta, kiitos. Vinkki laventamisen paikan muistamiseen (kolmas video): Laventaminen -> Left. Tai aakkosjärjestys: laventaminen tulee ennen supistamista. 🙂
Kiitos Kati!
Moikka! Minua vaivaa se, että eihän h ikinä saavuta arvoa 0? Se vain lähestyy sitä. Joten eikö tuo ole tavallaan väärin sijoittaa nolla lausekkeeseen?
Kyseessä on raja-arvo kun h lähestyy nollaa eli h:n arvo menee äärettömän lähelle nollaa, mutta ei ikinä saavuta sitä. Koska h ei ole nolla, se voidaan supistaa pois murtolausekkeesta, jolloin usein jää lauseke, jossa h ei ole nimittäjässä. Tällöin raja-arvon selvittämiseksi voidaan sijoittaa lausekkeeseen h = 0, koska h:n arvo on niin lähellä nollaa kuin mahdollista. (Oikeastaan h on surreaaliluku epsilon (tai sen vastaluku), joka on suurempi kuin 0 ja pienempi kuin mikään positiivinen reaaliluku. Tätä ei kuitenkaan tarvitse osata lukiossa.)